The double meaning of 'completeness'

The expressions complete and its negation incomplete appear in two different meanings with respect to a logical system. It would be better if a system were called:

proof-incomplete     if there are true sentence strings that cannot be proven within the system

basis-incomplete     if there are sentence strings that that do not contradict the system,

                                     nor do their negations contradict the system

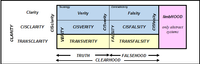
Sentences can be classified with respect to TRUTH as shown in the following figure:

The TRUTH of a Clarity needs at most limitive logic (predicate logic with limited quantions).

The TRUTH of a CISCLARITY sentence needs a special proof and quantive logic (predicate logic).

The TRUTH of a TRANSCLARITY sentence cannot be found within the calcule.

 For a proof-incomplete system the yellow area of TRANSCLARITY is not empty: there are true sentences like the famous Gödel-sentence (of Gödel's so-called 'incompleteness theorem') that cannot be proven from axioms.

In a basis-complete system it holds that every sentence is either a TRUTH or a FALSEHOOD : e.g. in Euclidean geometry every sentence is either true or false, tertium non datur. In a basis-incomplete system the purple area of limbHOOD is not empty: there are sentences that are neither true nor false, they are so to speak in limbo. The simple basis-incomplete example of absolute geometry theory can be made basis-complete by adding an axiom of parallelity. This is not the case for the famous example of axiomatic set theory with the sentence of Cantor's continuum hypothesis that shows that it is not basis-complete.